analysis: analysis::C2Functions::C2Function::partial

def partial_integrals	(	self,
		recur_data,
		args
	)

For points in recur_data, compute {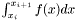 $\int_{x_i}^{x_{i+1}} f(x) dx$ } .

Note: The length of the return is one less than the length of recur_data. partial_integrals() uses a method with an error O(dx**10) with full information from the derivatives.

the integration is adaptive, starting from the grid provided, and returning data in the intervals between the grid points.

Parameters:

	recur_data	grid defining the subdomains over which the integral is computed, and hints for the adaptive algorithm (on initial call)
	absolute_error_tolerance	total absolute error allowed on each explicit subdomain
	relative_error_tolerance	total relative error allowed on each explicit subdomain
	derivs	how much continuity? derivs=2 => full method, 1 => less smooth function, 0 => Simpson's rule
	allow_recursion	allow adaptive behavior if true, otherwise just use subdomains provided
	extrapolate	carry out simple Richardson-Romberg extrapolation if true

Returns:

vector in which results from subdomains are returned.

def partial_integrals(self, xgrid, relative_error_tolerance=1e-12, derivs=2, 
    absolute_error_tolerance=1e-12, depth=0, debug=0, extrapolate=1, allow_recursion=True)
    Return the integrals of a function between the sampling points xgrid.  
    The sum is the definite integral.
    The choices for derivs are 0, 1 or 2, anything else is an error.
    The derivs parameter is used as follows: 
derivs=0 uses Simpsons rule (no derivative information).   
derivs=1 uses a 6th order technique based the first derivatives, but no second derivatives
derivs=2 uses a 9th (really 10th, since the 9th order error vanishes by symmetry) 
    order tehcnique based the first and second derivatives.
Be very aware that the 9th order method will only really benefit with very smooth functions, 
    but then it is magic!

Definition at line 316 of file C2Functions.py.

00316                                                    :
00317         """def partial_integrals(self, xgrid, relative_error_tolerance=1e-12, derivs=2, 
00318             absolute_error_tolerance=1e-12, depth=0, debug=0, extrapolate=1, allow_recursion=True)
00319             Return the integrals of a function between the sampling points xgrid.  
00320             The sum is the definite integral.
00321             The choices for derivs are 0, 1 or 2, anything else is an error.
00322             The derivs parameter is used as follows: 
00323                 derivs=0 uses Simpsons rule (no derivative information).   
00324                 derivs=1 uses a 6th order technique based the first derivatives, but no second derivatives
00325                 derivs=2 uses a 9th (really 10th, since the 9th order error vanishes by symmetry) 
00326                     order tehcnique based the first and second derivatives.
00327                 Be very aware that the 9th order method will only really benefit with very smooth functions, 
00328                     but then it is magic!
00329         """
00330     
00331         if type(recur_data[1]) is not tuple:    #this is an initialization call, set everything up
00332             funcgrid=[ ( (x, )+ self.value_with_derivatives(x) ) for x in recur_data ] 
00333             self.total_func_evals=len(recur_data)
00334             
00335             derivs= args.get('derivs', 2)
00336             if derivs==0:
00337                 eps_scale, extrap_coef= 0.1, 16.0
00338             elif derivs==1:
00339                 eps_scale, extrap_coef = 0.1, 64.0
00340             elif derivs==2:
00341                 eps_scale, extrap_coef = 0.01, 1024.0
00342             
00343             else:
00344                 raise C2Exception("derivs passed to partial_integrals, must be 0, 1 or 2, got %d" % derivs)
00345 
00346             allow_rec= args.get('allow_recursion', True)
00347             extrapolate = args.get('extrapolate', True) and allow_rec #can only extrapolate after recursion
00348             
00349             recur_data=[0, funcgrid, ( ),
00350                     args.get('absolute_error_tolerance', 1e-12),
00351                     args.get('relative_error_tolerance', 1e-12),
00352                     args.get('debug', 0),
00353                     extrapolate, derivs, eps_scale, extrap_coef, allow_rec
00354                 ]           
00355         
00356         (depth, funcgrid, old_integrals, absolute_error_tolerance, relative_error_tolerance, 
00357                 debug, extrapolate, derivs, eps_scale, extrap_coef, allow_rec)=recur_data
00358         
00359         retvals=[0.0]*(len(funcgrid)-1)
00360         
00361         for i in range(len(funcgrid)-1):
00362             x0, y0, yp0, ypp0=funcgrid[i]
00363             x2, y2, yp2, ypp2=funcgrid[i+1]
00364             x1=0.5*(x0+x2)
00365             y1, yp1, ypp1=self.value_with_derivatives(x1)
00366             self.total_func_evals+=1
00367             dx=x2-x0
00368             dx2=0.5*dx
00369 
00370             #check for underflow on step size, which prevents us from achieving specified accuracy. 
00371             if abs(dx) < abs(x1)*relative_error_tolerance:
00372                 raise C2Exception("Step size underflow in partial_integrals, depth = %d, x = %.4f" %
00373                         (depth, x1))
00374             
00375             #if we are below the top level, the previous term is already computed.  
00376             # Otherwise, compute it to one lower order
00377             if  old_integrals:
00378                 total=old_integrals[i]
00379             elif derivs==2:
00380                 total=( (14*y0 + 32*y1 + 14*y2) +  dx * (yp0 - yp2) ) * dx /60.
00381 
00382             elif derivs==1:
00383                 total=(y0+4.0*y1+y2)*dx/6.0
00384             else:
00385                 total=0.5*(y0+y2)*dx
00386 
00387             if derivs==2:
00388                 #use ninth-order estimates for each side. (Thanks, Mathematica!)
00389                 left=   ( ( (169*ypp0 + 1024*ypp1 - 41*ypp2)*dx2 + (2727*yp0 - 5040*yp1 + 423*yp2) )*dx2 + 
00390                         (17007*y0 + 24576*y1 - 1263*y2) )* (dx2/40320.0)
00391                 right=  ( ( (169*ypp2 + 1024*ypp1 - 41*ypp0)*dx2 - (2727*yp2 - 5040*yp1 + 423*yp0) )*dx2 + 
00392                         (17007*y2 + 24576*y1 - 1263*y0) )* (dx2/40320.0)
00393             elif derivs==1:
00394                 left=   ( (202*y0 + 256*y1 + 22*y2) + dx*(13*yp0 - 40*yp1 - 3*yp2) ) * dx /960.
00395                 right=  ( (202*y2 + 256*y1 + 22*y0) - dx*(13*yp2 - 40*yp1 - 3*yp0) ) * dx /960.
00396             else:
00397                 left=   (5*y0 + 8*y1 - y2)*dx/24.
00398                 right=  (5*y2 + 8*y1 - y0)*dx/24.
00399 
00400             eps= abs(total-(left+right))*eps_scale 
00401             #the real error should be 2**order times smaller on this iteration, be conservative
00402             if extrapolate:
00403                 eps=eps*eps_scale 
00404                 #gain another factor of 2**order if extrapolating (typical), but be conservative
00405                 
00406             if  (not allow_rec) or eps < absolute_error_tolerance or eps < abs(total)*relative_error_tolerance:
00407                 if not extrapolate:
00408                     retvals[i]=left+right
00409                 else:
00410                     retvals[i]=(extrap_coef*(left+right) - total) / (extrap_coef-1) 
00411                     #since h fell by 2, h**6=64, and we are extrapolating in h**6
00412                 if debug==1: 
00413                     print "accepted results at depth ", depth,  "x, dx = %7.3f, %10.6f" % (x1, dx), 
00414                     print "scaled error = ", eps/ (abs(total)*relative_error_tolerance)
00415             else:
00416                 if debug==1: 
00417                     print "rejected results at depth ", depth,  "x, dx = %7.3f, %10.6f" % (x1, dx), 
00418                     print "scaled error = ", eps/ (abs(total)*relative_error_tolerance)
00419                 recur_data[0:4]=(depth+1, (funcgrid[i], (x1, y1, yp1, ypp1), funcgrid[i+1]), 
00420                         (left, right), absolute_error_tolerance/2 )
00421                 l, r =self.partial_integrals(recur_data)
00422                 retvals[i]=l+r
00423         if debug ==2:
00424             print "\nintegrating at depth ", depth
00425             print xgrid
00426             print funcgrid
00427             import operator
00428             print retvals
00429             if old_integrals: 
00430                 print map(operator.sub, old_integrals, retvals)
00431             print "\nreturning from depth ", depth
00432         return retvals
00433 
    ##